NCERT Solutions Class 8 Maths Chapter 3 Excercise 3.2 Understanding Quadrilaterals
Class 8 Maths Exercise 3.2 Solutions
Class 8 Maths Exercise 3.2 in Hindi
Class 8 Maths Book Download in PDF
Class 8 Maths Chapter 3 Solutions
Class 8 Maths NCERT Solutions
Class 8 All Subjects Solutions
NCERT Solutions for Class 8 Maths Chapter 3 Exercise 3.2 in Hindi and English Medium modified and updated for academic year 2024-25. The question answers and explanations of ex. 3.2 of 8th Maths are revised according to new syllabus and revised NCERT books for 2024-25 exams.
Class 8 Mathematics Chapter 3 Exercise 3.2 Solution
Download the free PDF file of Class VIII Mathematics NCERT book, Exercise 3.2 of chapter 3 Understanding Quadrilaterals. All the solutions for the questions in exercise 3.2 of class 8 mathematics are presented in a step-by-step manner. Our CBSE solutions are provided in a simple and easy-to-understand way. If you encounter any issues while using the NCERT Solution App or website, feel free to contact us without any hesitation.
Image
| Class 8: | Mathematics |
| Chapter 3 | Excercise 3.2 |
| Chapter Name | Udnerstanding Quadrilaterals |
| Content Type | Videos, Images and Text Format |
| Medium | Hindi and English Medium |
| Academic Session | 2024-25 |
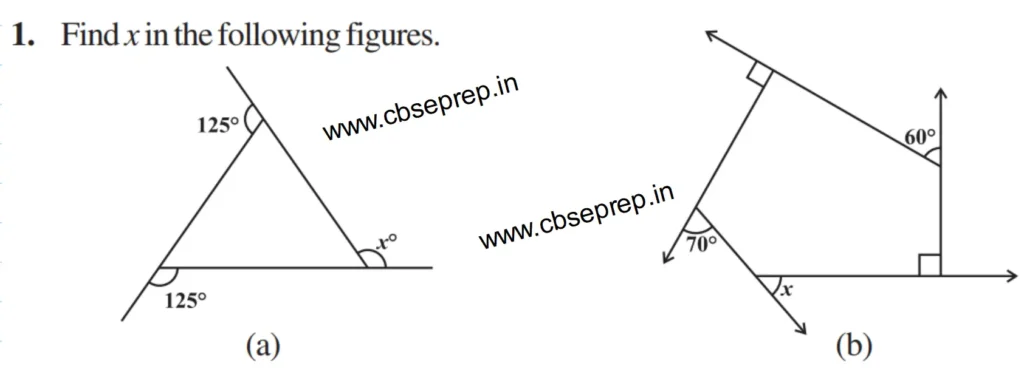
Q.1
Solution:-
Solutions:-
(a)
We know that the sum of all the exterior angles of a polygon = 360°
As per the Question
=≫ 125° + 125° + x° = 360°
=≫ x° = 360° – 125° – 125°
=≫ x° = 110°
(b)
As per the Question
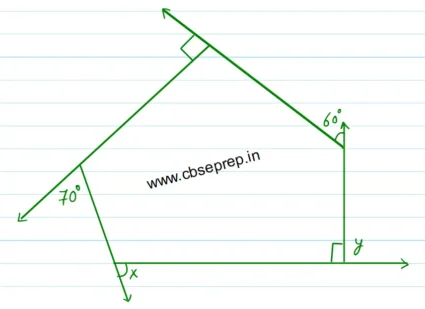
Let’s assum one of the exterior angle besides 90° interior angles as Y°
=≫ Y° + 90° = 180° [The sum of the supplementary angles is 180°] or [Linera Pair]
=≫ Y° = 180° – 90° = 90°
We know that the sum of all the exterior angles of a polygon = 360°
as per the question
=≫ x° + Y° + 60° + 90° + 70° = 360°
=≫ x° + 90° + 60° + 90° + 70° = 360°
=≫ x° = 360° – 90° – 60° – 90° – 70°
=≫ x° = 360° – 310°
=≫ x° = 50°
Question 2 Ex. 3.2 Maths
Find the measure of each exterior angle of a regular polygon of
(i) 9 sides
(ii) 15 sides
Solution:-
(i) As we all know the sum of the exterior angles of a polygon is 360°
Measure of each angle of a 9 sided polygon
=≫ Sum of exterior angles/sides
=≫ 360°/9
=≫ 40°
(ii) As we all know the sum of the exterior angles of a polygon is 360°
Measure of each angle of a 15 sided polygon
=≫ Sum of exterior angles/sides
=≫ 360°/15
=≫ 24°
Question 3 Ex. 3.2 Maths
How many sides does a regular polygon have if the measure of an exterior angle is 24°
Solution:-
As we all know the sum of the exterior angles of a polygon is 360°
Sides of a regular polygon haveing an exterior angle 24° is
=≫ Sum of exterior angles/measure of an exterior angle
=≫ 360°/24°
=≫ 15 sides
Question 4 Ex. 3.2 Maths
How many sides does a regular polygon have if each of its interior angles is 165°
Solution:-
Each exterior angle = 180° – Interior angle
= 180° – 165°
= 15°
As we all know the sum of the exterior angles of a polygon is 360°
Sides of a regular polygon haveing an exterior angle 15° is
=≫ Sum of exterior angles/measure of an exterior angle
=≫ 360°/15°
=≫ 24 sides
Question 5 Ex. 3.2 Maths
(a) Is it possible to have a regular polygon with measure of each exterior angle as 22°
(b) Can it be an interior angle of a regular polygon? Why?
Solution (a)
Each exterior angle = 22
Sum of all exterior angles = 360
Sides of a regular polygon haveing an exterior angle 22° is
=≫ Sum of exterior angles/measure of an exterior angle
=≫ 360°/22°
=≫ 16.36 (Which is not a whole number)
Therefore, a regular polygon with measure of each exterior angle 22 is not possible as 22° is not the divisor of 360°
Solution (b)
Each exterior angle = 180° – Interior angle
= 180° – 22°
= 158°
As we all know the sum of the exterior angles of a polygon is 360°
Sides of a regular polygon haveing an exterior angle 158° is
=≫ Sum of exterior angles/measure of an exterior angle
=≫ 360°/158°
=≫ 2.27 (Which is not a whole number)
Therefore, a regular polygon with measure of each exterior angle 158° is not possible as 158° is not the divisor of 360°.
Question 6 Ex. 3.2 Maths
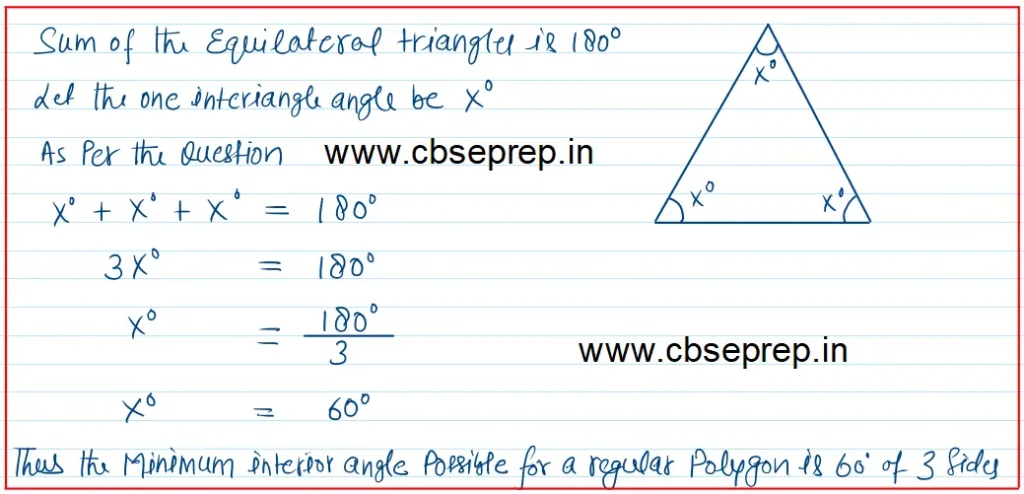
(a) What is the minimum interior angle possible for a regular polygon? Why?
(b) What is the maximum exterior angle possible for a regular polygon?
Solution (a):-
The Minimum Interior angles is possible with with smallest regular polygon. The smallest regular polygon is the equilateral traiable with 3 sides.