[NCERT] Class 8 Maths Ex. 3.3 Understanding Quadrilaterals Solutions

[NCERT] Class 8 Maths Ex. 3.3 Understanding Quadrilaterals Solutions (2024-25)

Given a parallelogram ABCD. Complete each statement along with the definition or property used.

(i) AD = _

(ii) ∠DCB = __

(iii) OC = _

(iv) m ∠DAB + ∠CDA = _

Solution:-

(i) AD = BC (Opposite side of a parallelogram are equal)

(ii) ∠DCB = ∠DAB (Opposite angles of a parallelogram are equal)

(iii) OC = AO = (Diagonals of a parallelogram bisects each other)

(iv) m∠DAB + m∠CDA = 180° (Adjacent angles in a parallelogram are supplementary)

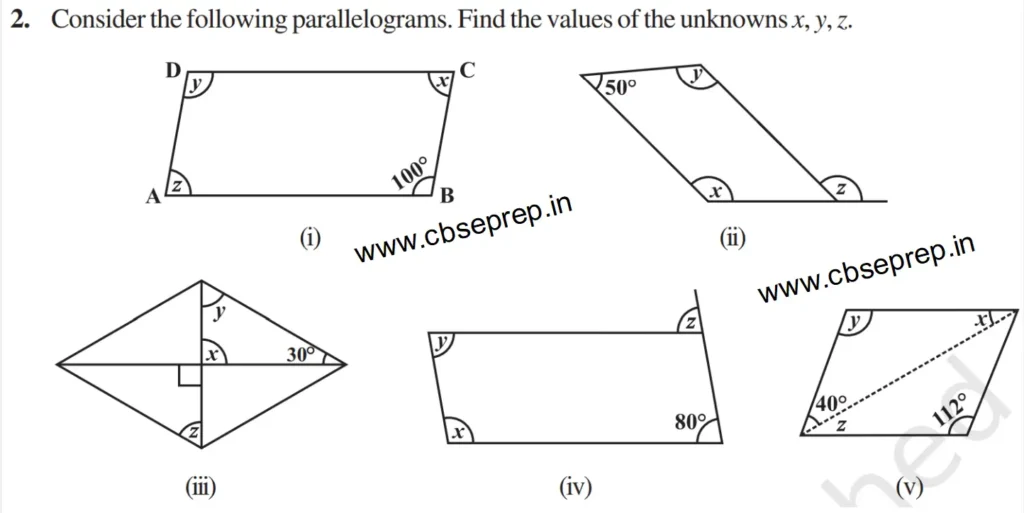
Solution (i)-

=≫ ∠y = ∠ABC = 100° (Opposite angles of a parallelograms are equal)

=≫ ∠x° + ∠ABC = 180° (Adjacent angles in a parallelogram are supplementary)

=≫ ∠x° + ∠100° = 180°

=≫ ∠x° = 180° – 100°

=≫ ∠x° = 80°

=≫ ∠z = ∠x° = 80° (Opposite angles of a parallelograms are equal)

Solution (ii):-

=≫ ∠x° + ∠50° = 180° (Adjacent angles in a parallelogram are supplementary)

=≫ ∠x° = 180° – ∠50°

=≫ ∠x° = 130°

=≫ ∠x° = ∠y° = 130° (Opposite angles of a parallelograms are equal)

Let the opposite angle of ∠50° is ∠a

=≫ ∠a = ∠50° (Opposite angles of a parallelograms are equal)

=≫ ∠a + ∠z = 180° (linear Pair)

=≫ 50° + ∠z = 180°

=≫ ∠z = 180° – 50°

=≫ ∠z = 130°

Solution (iii):-

∠x° = 90° (vertically opposite angles are equal)

∠x° + ∠y + 30° = 180° (angle sum property of a triangle)

90° + ∠y° + 30° = 180°

∠y° = 180° – 90° – 30°

∠y° = 60°

∠y° = ∠z° = 60° (alternate interior angles are equal)

Solution (iv):-

∠y° = 80° (opposite angles of a parallelogram are equal)

∠x° + 80° = 180° (Adjacent angles in a parallelogram are supplementary)

∠x° = 180° – 80°

∠x° = 100°

Let the opposite angle of ∠x° be ∠a°

∠a° = ∠x° = 100° (Opposite angles of IIgm are equal)

∠a° + ∠z° = 180° (Linear Pair)

100° + ∠z° = 180°

∠z° = 180° – 100°

∠z° = 80°

Solution (v):-

∠y° = 112° (opposite angles of a parallelogram are equal)

∠x° + ∠y° + 40° = 180° (angle sum property of a triangle)

∠x° + ∠112° + 40° = 180°

∠x° = 180° – 112° – 40°

∠x° = 28°

∠z° = ∠x° = 28° (interior opposite angles are equal)

Final Answers

∠x° = 28°, ∠y° = 112°, ∠z° = 28°

Solution:-

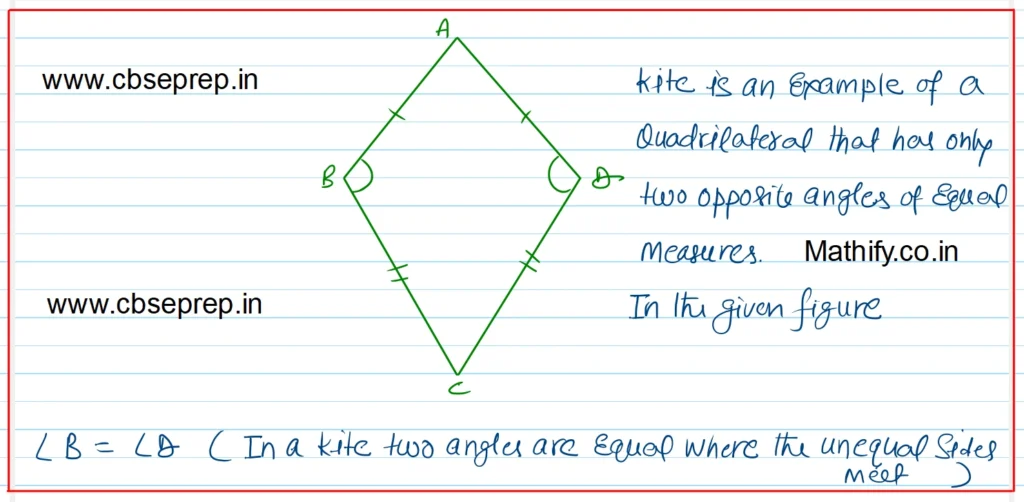
Solution:-

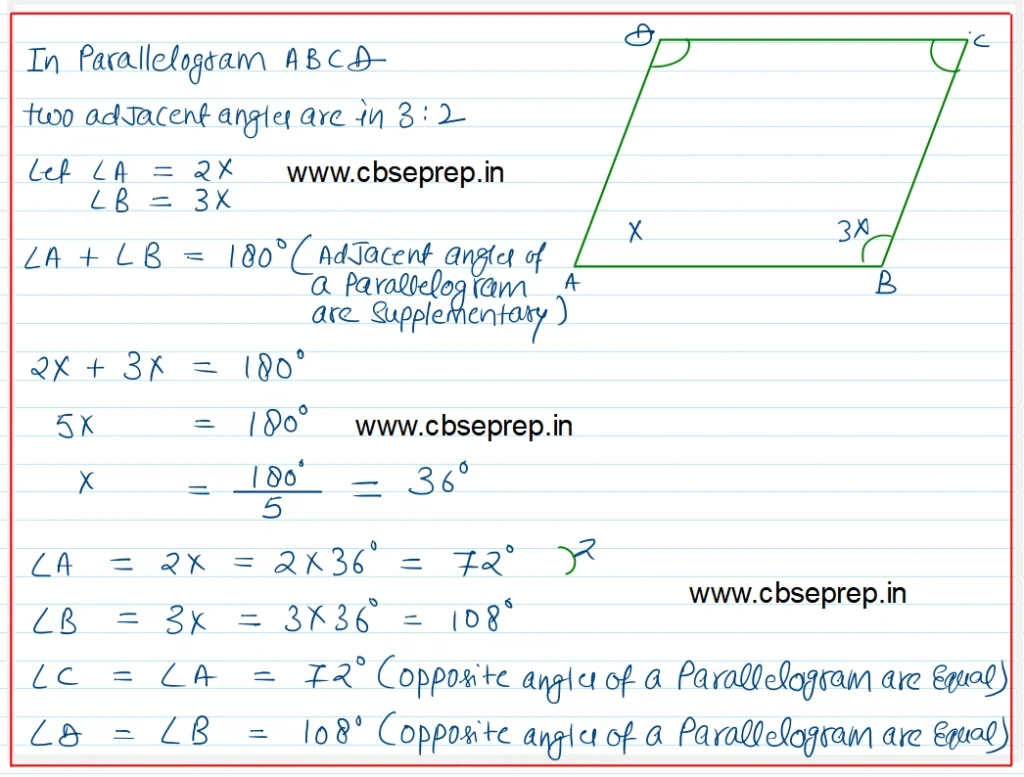
Solution:-

Solution:-

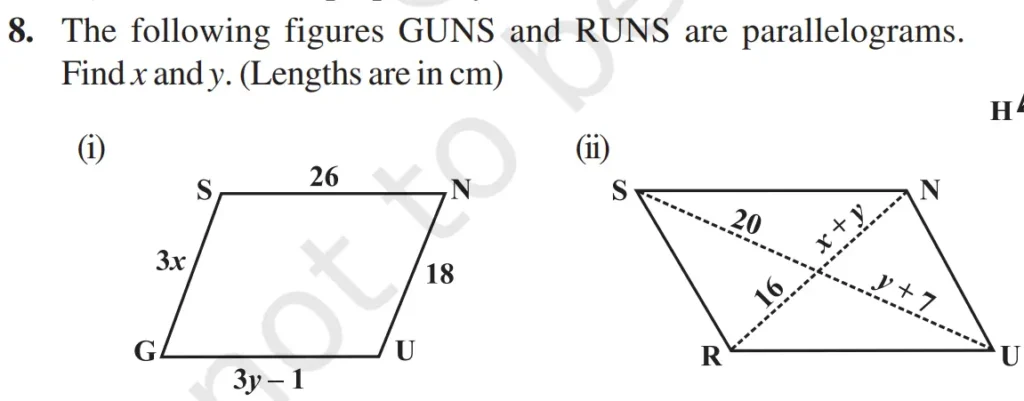
Solution:-

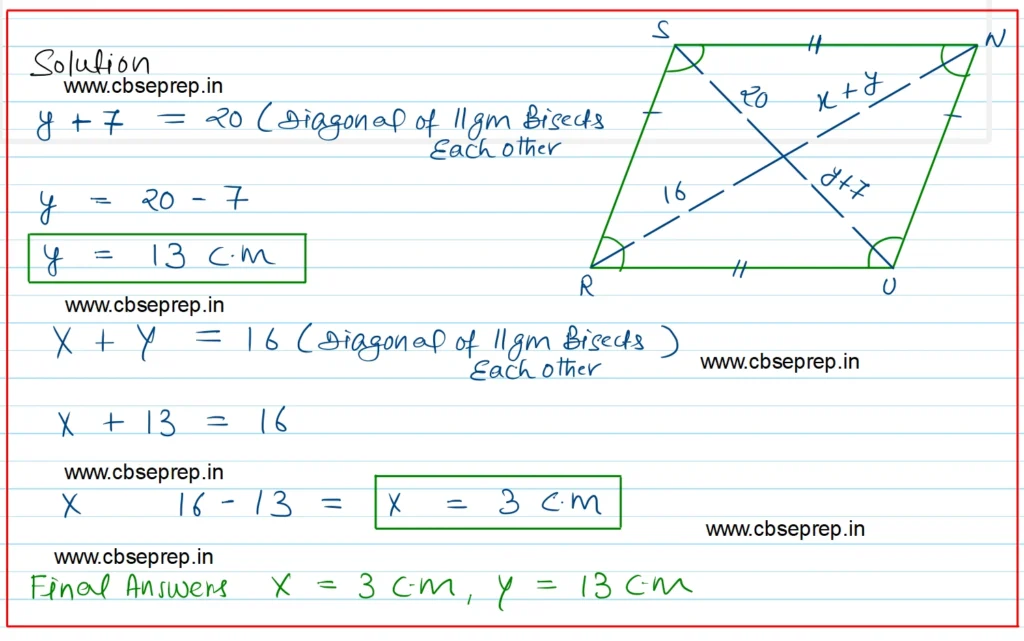
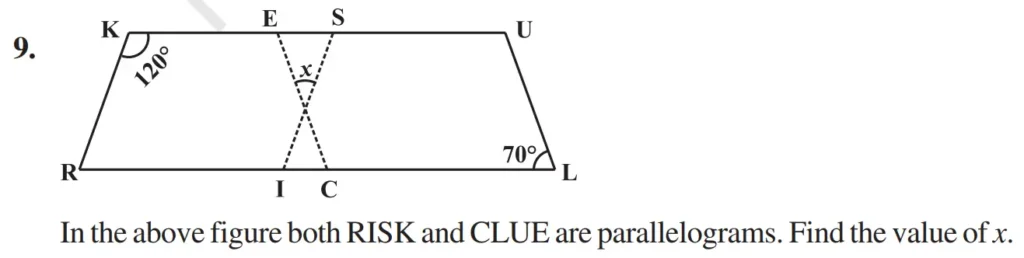
Solution:-

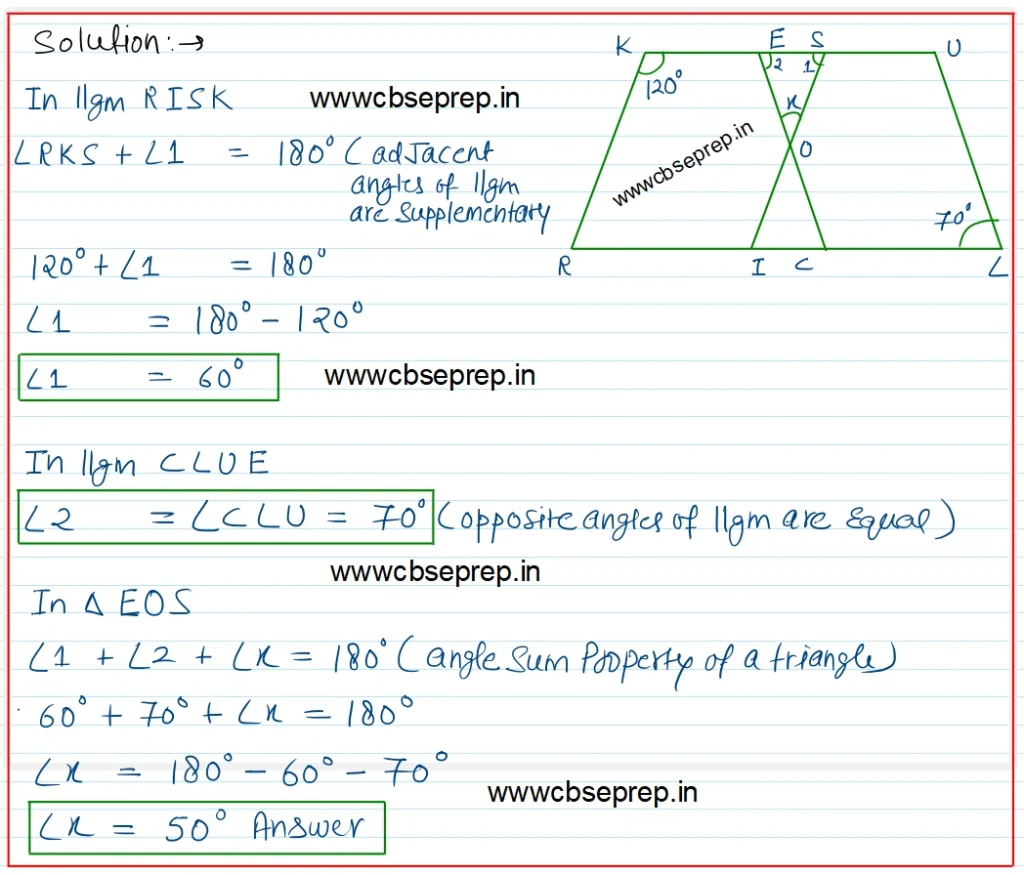
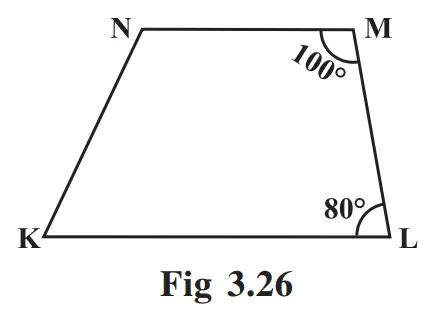
Solution:-

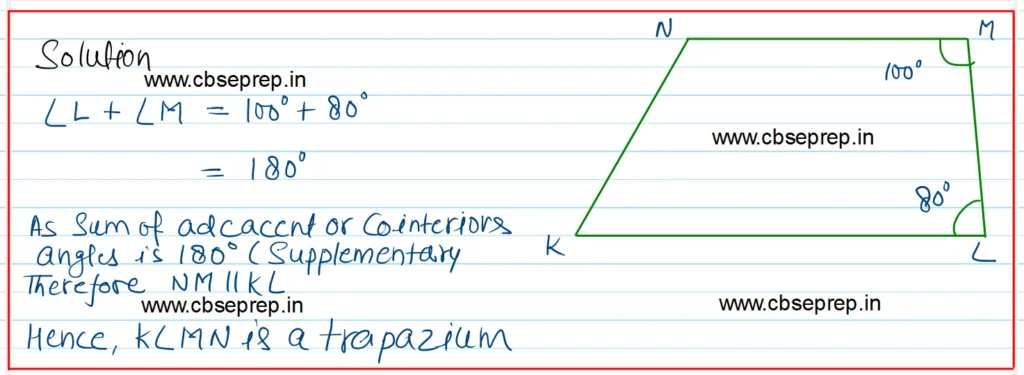
Solution:-

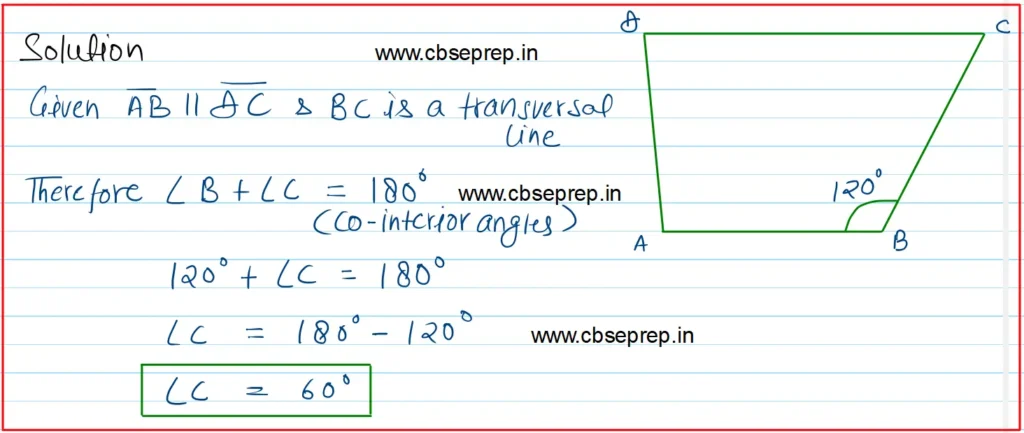
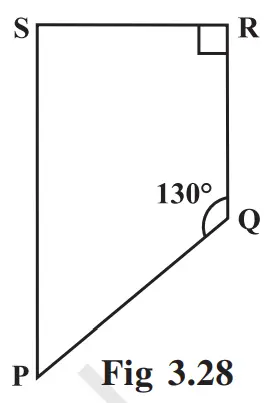
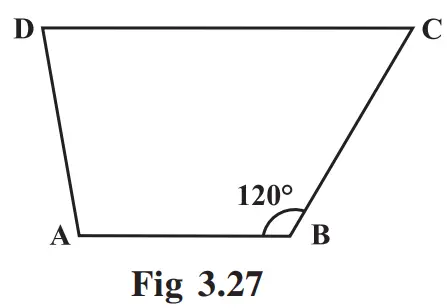
Solution:-