NCERT Science Class 9 Chapter 7 Question Answer Solutions – Motion FREE PDF Download 2025-26
Page – 74
Q. 1. An object has moved through a distance. Can it have zero displacement? If yes, support your answer with an example.
Answer:-
Yes, an object can have zero displacement even if it has moved through a certain distance. This happens when the object starts and ends at the same position.
Explanation 🧐
- Distance refers to the total path traveled by an object, irrespective of direction.
- Displacement is the shortest straight-line distance between the initial and final positions of the object.
Example ✅
Imagine a person walking 10 meters forward and then coming back 10 meters to the starting point.
- Total Distance traveled = 10 m (forward) + 10 m (backward) = 20 m
- Displacement = Final position – Initial position = 0 m (since the person returns to the starting point)
Conclusion 🌟
Even though the person has traveled a distance of 20 meters, the displacement is zero because the initial and final positions are the same.
Q. 2. A farmer moves along the boundary of a square field of side 10 m in 40s. What will be the magnitude of displacement of the farmer at the end of 2 minutes 20 seconds from his initial position?
Answer:-


Q. 3. Which of the following is true for displacement?
(a) It cannot be zero.
(b) Its magnitude is greater than the distance travelled by the object.
Answer:-
Answer with Explanation 📚✨
✅ Correct Statement: Neither (a) nor (b) is true!
Let’s analyze both statements carefully:
🚫 (a) It cannot be zero – Incorrect!
Displacement can be zero if an object returns to its initial position after moving.
- Example: If a person walks 10 meters forward and then 10 meters back to the starting point, the total displacement = 0 m, even though distance traveled is 20 m.
🚫 (b) Its magnitude is greater than the distance traveled by the object – Incorrect!
- Displacement is the shortest straight-line distance between the initial and final positions.
- Distance is the total length of the path traveled.
- Since displacement can never be more than the actual distance traveled, this statement is false.
✅ Final Conclusion:
Displacement can be zero, and it is always less than or equal to the distance traveled! 🌟
Page – 76
Q. 1. Distinguish between speed and velocity.
Answer:-
Difference Between Speed and Velocity 🚗⚡
| 🔹 Aspect | 🚀 Speed | 🏹 Velocity |
|---|---|---|
| Definition 📖 | Distance traveled per unit time. | Displacement per unit time in a specific direction. |
| Formula 🧮 | Speed = Distance / Time | Velocity = Displacement / Time |
| Vector or Scalar? 🔄 | Scalar (has only magnitude, no direction) | Vector (has both magnitude and direction) |
| Can be Negative? ❌ | No, speed is always positive or zero. | Yes, velocity can be negative, positive, or zero based on direction. |
| Example 🏃♂️ | A car moving at 40 km/h. | A car moving 40 km/h towards North. |
Key Conclusion ✨
✅ Speed tells us how fast an object is moving, but velocity includes both speed and direction!
✅ Velocity changes when either the magnitude or direction changes!
Q. 2. Under what condition(s) is the magnitude of average velocity of an object equal to its average speed?
Answer:-
Condition for Average Velocity = Average Speed 🚗⚡
✅ The magnitude of average velocity is equal to average speed only when an object moves in a straight line in a single direction without changing its path.
Key Explanation 📖
1️⃣ Average Speed = Total distance traveled ÷ Total time
2️⃣ Average Velocity = Total displacement ÷ Total time
🔹 Since displacement is the shortest straight-line distance between the initial and final positions, it equals the distance traveled only in straight-line motion!
Example 🚀
If a car moves 100 meters east in 10 seconds,
- Distance traveled = 100 m
- Displacement = 100 m (since it didn’t change direction)
- Average speed = 100/10 = 10 m/s
- Average velocity = 100/10 = 10 m/s (since displacement = distance)
✅ Conclusion 🌟
The object must move in a straight line, without reversing or changing direction, for its average velocity to be equal to its average speed.
Q. 3. What does the odometer of an automobile measure?
Answer:-
Odometer: What Does It Measure? 🚗⚙️
✅ Definition:
An odometer is a device in automobiles that measures the total distance traveled by the vehicle. It is usually displayed on the dashboard.
Key Explanation 📖
- The odometer keeps track of the cumulative distance covered by the vehicle from the time it starts operating. 🚙📏
- It helps in maintenance schedules, fuel efficiency checks, and resale valuation of the vehicle. 💡🔧
- The reading increases as the vehicle moves forward but never decreases. ⬆️🚦
Units of Measurement 📏
- The distance is measured in kilometers (km) or miles (mi), depending on the region. 🌍📌
Example 🚀
If a car has traveled 5,000 km in total since it was manufactured, the odometer reading will be 5,000 km! 🏁✨
✅ Conclusion:
The odometer measures distance traveled, not speed or displacement! It is crucial for vehicle monitoring and maintenance. 🚘🔍
Q. 4. What does the path of an object look like when it is in uniform motion?
Answer:-
Path of an Object in Uniform Motion 🚀✨
✅ Definition:
An object is said to be in uniform motion when it covers equal distances in equal intervals of time without changing its speed or direction. ⏳📏
What Does the Path Look Like? 👀
The path of an object in uniform motion is always a straight line if it moves in a single direction. 🏹➡️
- If the object moves along a straight road or a railway track, its path remains linear (straight). 🚗🛤️
- If the object moves in a circular path (like Earth’s motion around the Sun 🌍☀️), its uniform motion follows a fixed curve.
Example 🚀
- A car moving at constant speed on a straight highway → Path is a straight line.
- A satellite orbiting the Earth at constant speed → Path is circular.
✅ Conclusion:
In uniform motion, an object’s path is straight if it moves in one direction, but it can be circular or curved if constrained by forces like gravity. 🌟
Q. 5. During an experiment, a signal from a spaceship reached the ground station in five minutes. What was the distance of the spaceship from the groundstation? The signal travels at the speed of light, that is, 3 × 108 ms–1.
Answer:-

Page – 74
Q. 1. When will you say a body is in (i) uniform acceleration? (ii) nonuniform acceleration?
Answer:-
Types of Acceleration 🚀📖
Acceleration refers to the rate of change of velocity of a body over time. Let’s distinguish between uniform and non-uniform acceleration!
(i) Uniform Acceleration 📈✨
✅ Definition: When a body’s velocity changes by an equal amount in equal intervals of time, it is said to be in uniform acceleration.
🔹 Key Features:
- The rate of acceleration remains constant. ⚖️
- The velocity increases or decreases smoothly. 🔄
🔹 Example:
- Freely falling object under gravity 🌍🪂
- A car speeding up at a constant rate 🚗💨
Formula for uniform acceleration:
[ a = \frac{\text{Change in Velocity}}{\text{Time Taken}} ]
(ii) Non-Uniform Acceleration ⚠️📉
✅ Definition: When a body’s velocity changes by an unequal amount in equal intervals of time, it is said to be in non-uniform acceleration.
🔹 Key Features:
- The acceleration varies at different points. 🔄
- The change in velocity is not constant. ❌
🔹 Example:
- A car moving in traffic, where speed changes randomly 🚦🚙
- A ball rolling on a rough surface, slowing down unevenly ⚽⬇️
Conclusion 🎯
✅ Uniform acceleration means constant change in velocity, while non-uniform acceleration means variable change in velocity.
Q. 2. A bus decreases its speed from 80 km h–1 to 60 km h–1 in 5 s. Find the acceleration of the bus.
Answer:-

Q. 3. A train starting from a railway station and moving with uniform acceleration attains a speed 40 km h–1 in 10 minutes. Find its acceleration.
Answer:-

Page – 81
Q. 1. What is the nature of the distance-time graphs for uniform and non-uniform motion of an object?
Answer:-
Nature of Distance-Time Graphs for Motion 📈🚗
The shape of a distance-time graph helps us understand whether an object’s motion is uniform or non-uniform! Let’s analyze both cases.
(i) Distance-Time Graph for Uniform Motion 📊✨
✅ Definition:
An object is in uniform motion when it covers equal distances in equal intervals of time.
✅ Graph Characteristics:
- The graph is a straight line sloping upward. 📈
- The slope remains constant, meaning the object moves with a constant speed.
🔹 Example: A car moving steadily at 60 km/h on a highway 🚗💨.
(ii) Distance-Time Graph for Non-Uniform Motion 📊⚠️
✅ Definition:
An object is in non-uniform motion when it covers unequal distances in equal intervals of time.
✅ Graph Characteristics:
- The graph is a curved line instead of a straight line. 🔄
- The slope varies, indicating a changing speed (acceleration or deceleration).
🔹 Example: A car starting from rest, then gradually increasing speed 🚦🚗⬆️.
Conclusion 🎯
✅ Uniform motion → Straight-line graph (constant speed).
✅ Non-uniform motion → Curved graph (changing speed).
📚 Tip: If acceleration is positive, the curve bends upward. If acceleration is negative, the curve bends downward!
Q. 2. What can you say about the motion of an object whose distance-time graph is a straight line parallel to the time axis?
Answer:-
Motion of an Object with a Distance-Time Graph Parallel to the Time Axis 📈🚀
✅ Key Observation:
If the distance-time graph is a straight line parallel to the time axis, it means that the distance remains constant over time. ⏳📏
Explanation 📖
- The object is not moving—it remains stationary! 🏠⚠️
- Since distance does not change, its speed is zero. 🚫⚡
- There is no displacement, meaning no motion occurs.
Example 🚗⏸️
If a car is parked on the roadside, its distance from a reference point remains unchanged over time. So, its distance-time graph will be a horizontal line parallel to the time axis.
Final Conclusion 🎯
✅ A straight horizontal line in a distance-time graph represents a stationary object that is not in motion.
Q. 3. What can you say about the motion of an object if its speedtime graph is a straight line parallel to the time axis?
Answer:-
Motion of an Object with a Speed-Time Graph Parallel to the Time Axis 📈🚗
✅ Key Observation:
If the speed-time graph is a straight line parallel to the time axis, it means that the object is moving with a constant speed without any acceleration. ⚡⏳
Explanation 📖
- Since the speed does not change, acceleration is zero (i.e., no increase or decrease in velocity). 🚫📉
- The object moves with uniform motion in a straight line. 🏎️➡️
- Velocity remains constant, meaning the direction of motion is unchanged.
Example 🚀✨
- A car moving at 60 km/h on a straight highway with the same speed throughout the journey 🚗🛣️.
- A train traveling at a fixed speed without speeding up or slowing down 🚆⚖️.
Final Conclusion 🎯
✅ A speed-time graph that is a straight horizontal line parallel to the time axis represents an object moving with uniform speed and zero acceleration!
Q. 4. What is the quantity which is measured by the area occupied below the velocity-time graph?
Answer:-
Quantity Measured by the Area Below a Velocity-Time Graph 📈🚗
✅ Answer:
The area occupied below the velocity-time graph represents the displacement of the object! 📏✨
Key Explanation 📖
- The velocity-time graph plots velocity on the y-axis and time on the x-axis. 🏹⏳
- The area under the graph gives the product of velocity × time, which equals displacement (since Displacement = Velocity × Time).
Case-wise Explanation ⚡
1️⃣ For Uniform Velocity (Straight-Line Graph) ⏳
- The area forms a rectangle. 📏
- Displacement = Base × Height = Velocity × Time.
2️⃣ For Uniformly Accelerated Motion (Sloping Graph) 📉
- The area forms a triangle + rectangle combination. ⬛🔺
- Displacement is calculated using the total area (using formulas for triangle and rectangle).
Example 🚀
If an object moves with a velocity of 5 m/s for 10 seconds, the area under the velocity-time graph will be:
[ \text{Displacement} = 5 \times 10 = 50 \text{ meters} ]
✅ So, the object covers 50 meters of displacement! 🎯
Conclusion 🌟
✅ The area under the velocity-time graph represents the displacement of the object!
Page – 82
Q. 1. A bus starting from rest moves with a uniform acceleration of 0.1 ms-2 for 2 minutes. Find
(a) the speed acquired,
(b) the distance travelled.
Answer:-


Q. 2. A train is travelling at a speed of 90 km h–1. Brakes are applied so as to produce a uniform acceleration of – 0.5 m s-2. Find how far the train will go before it is brought to rest.
Answer:-

Q. 3. A trolley, while going down an inclined plane, has an acceleration of 2 cm/s-2. What will be its velocity 3 s after the start?
Answer:-

Q. 4. A racing car has a uniform acceleration of 4 m s-2. What distance will it cover in 10 s after start?
Answer:-

Q. 5. A stone is thrown in a vertically upward direction with a velocity of 5 m/s2. If the acceleration of the stone during its motion is 10 m s–2 in the downward direction, what will be the height attained by the stone and how much time will it take to reach there?
Answer:-


Back Exercise Question & Answer
Q. 1. An athlete completes one round of a circular track of diameter 200 m in 40 s. What will be the distance covered and the displacement at the end of 2 minutes 20s?
Answer:-

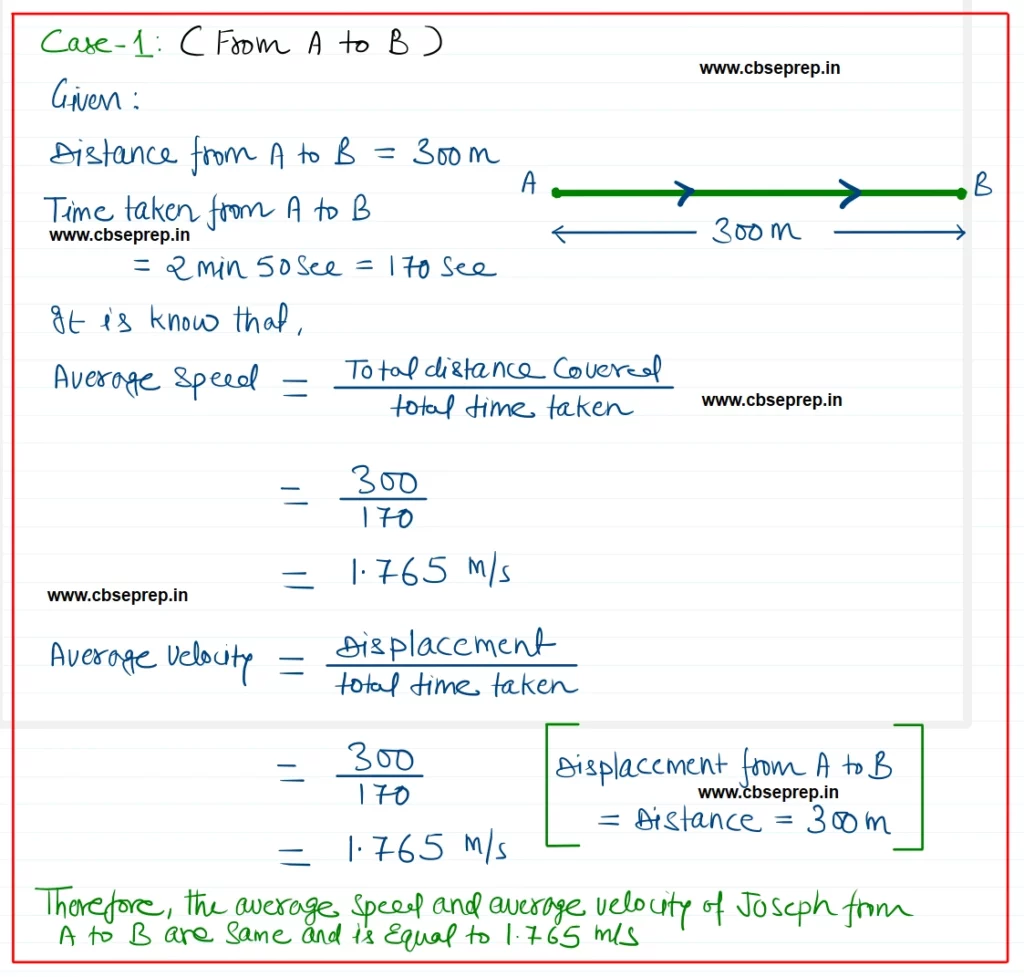
Q. 2. Joseph jogs from one end A to the other end B of a straight 300 m road in 2 minutes 30 seconds and then turns around and jogs 100 m back to point C in another 1 minute. What are Joseph’s average speeds and velocities in jogging (a) from A to B and (b) from A to C?
Answer:-

Q. 3. Abdul, while driving to school, computes the average speed for his trip to be 20 km h–1. On his return trip along the same route, there is less traffic and the average speed is 30 km h–1. What is the average speed for Abdul’s trip?
Answer:-


Q. 4. A motorboat starting from rest on a lake accelerates in a straight line at a constant rate of 3.0 m s–2 for 8.0 s. How far does the boat travel during this time?
Answer:-

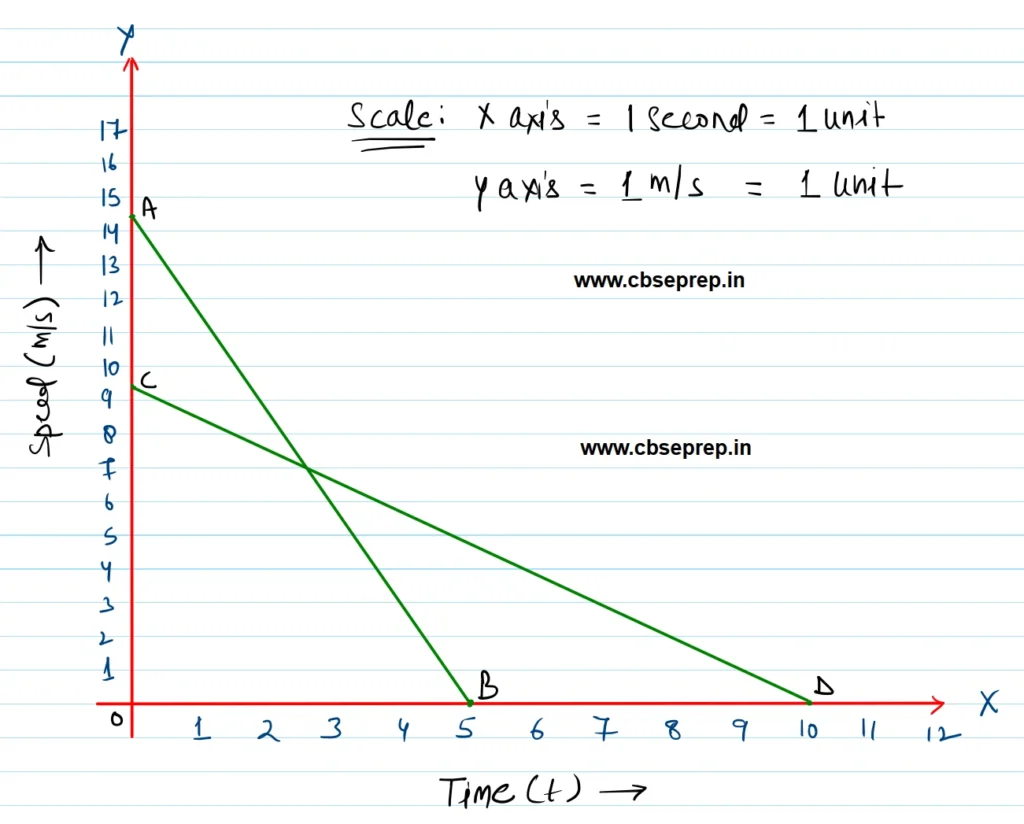
Q. 5. A driver of a car travelling at 52 km h–1 applies the brakes and accelerates uniformly in the opposite direction. The car stops is 5 s. Another driver going at 3 Kmh-1 in another car applies his brakes slowly and stops in 10s. On the same graph paper, plot the speed versus time graphs for the two cars. Which of the two cars travelled farther after the brakes were applied?
Answer:-




Q. 6. Fig 7.10 shows the distance-time graph of three objects A,B and C. Study the graph and answer the following questions:
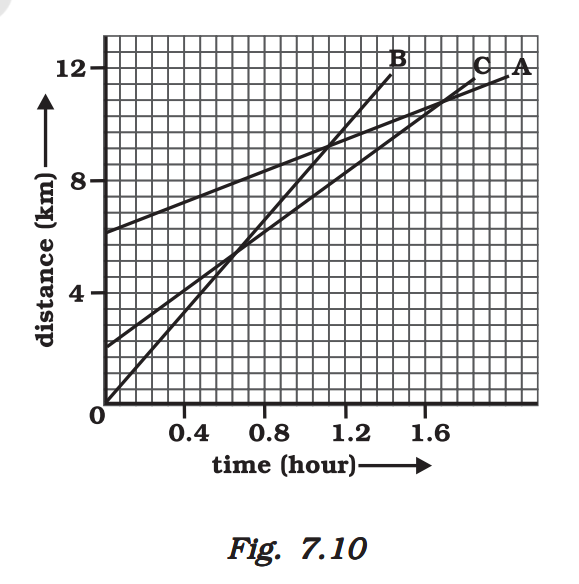
(a) Which of the three is travelling the fastest?
Ans:-
The slope of distance-time graph of moving object indiacates its speed. Greater the slope, higher is the speed. Now, in the given figure, the slope of distance-time graph of object B is the maximum, so the object B has the maximum speed. In other words, the object B is travelling the fastest.
(b) Are all three ever at the same point on the road?
Ans:-
In order to be at the same point on the road, the respective distance and time values for all the three moving objects should be the same. Since the distance time graph lines of the three objects A, B and C do not cross at a single point, therefore, the three objects are never at the same point on the road.
(c) How far has C travelled when B passes A?
Ans:-
We can see from the given figure that whenn B passes A at point D, then the C is at point E. If we locate the distance corresponding to point E on the Y-axis, we find that it is 6.5 Km. Thus C has travelled 6.5 Km when B passes A.
(d) How far has B travelled by the time it passes C?
Answer:-
Q. 7. A ball is gently dropped from a height of 20 m. If its velocity increases uniformly at the rate of 10 ms-2, with what velocity will it strike the ground? After what time will it strike the ground?
Answer:-


Q. 8. The speed-time graph for a car is shown is Fig. 7.11.
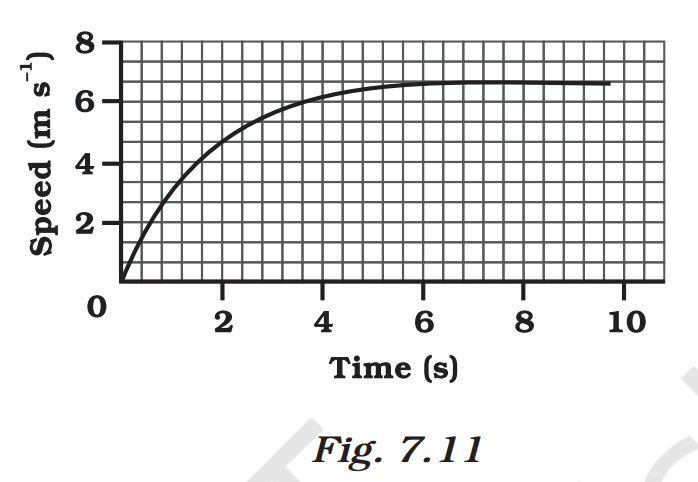
(a) Find how far does the car travel in the first 4 seconds. Shade the area on the graph that represents the distance travelled by the car during the period.
(b) Which part of the graph represents uniform motion of the car?
Answer:-
(a) The distance travelled by the car in the first 4 seconds is given by the area between the speet-time curve and the time axis from t = 0 to t= 4 second. This area of the distance time graph which reprsents the distance travelled by the car has been shaded in the graph shown below.
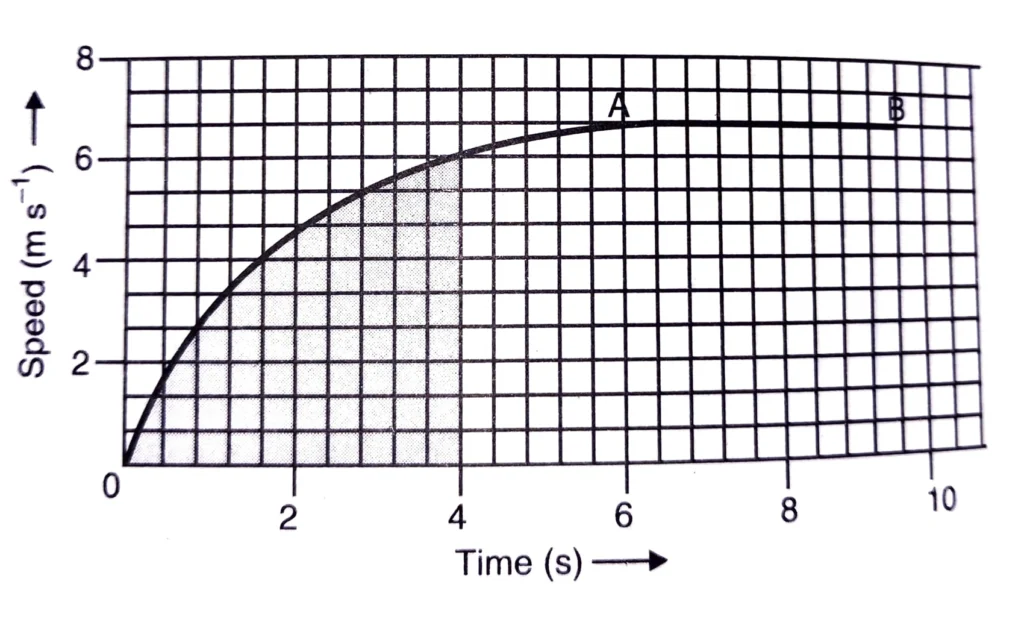
In order to find the distance travelled by the car in the first 4 seconds, we hae to count the number of squares in the shaded part of the graph and also calculate the distance represeneted by one square of the graph paper. While counting the number of squares in the shaded part of the graph, the squares which are half or more than half are counted as complete squares but the squares which are less than half are not counted. When counted in this way, the total number of squares in the shaded part of the graph is found to be 62.
We will now calcualte the distance represeneted by 1 square of the graph. This can be done as follows:
If we look at the X-axis, we find that 5 squares on X-axis represent a time of 2 seconds.
Now, 5 squares on X-axis – 2 s
1 square on X-axis = 2/5 s
Again, if we look at the Y-axis, we find that 3 squares on Y-axis represnt a speed of 2 m/s.
Now, 3 squres on Y-axis = 2 m/s
1 squre on Y-axis = 2/3 m/s
Since 1 square on X-axis represents 2/5 s and 1 square on Y-axis represents 2/3 m/s, therefore:
Area of 1 square on graph represents a distance = 2/5 s x 2/3 m/s = 4/15 m
Now, 1 square represents distance = 4/15 m
So, 63 squares represent distance = 4/15 x 63 m = 16.8 m
Thus, the car travels a distance of 16. 8 metres in the first 4 seconds.
(b) In uniform motion, the speed of car becomes constant. The constant speed is represented by a speed thime graph line which is parallel to the time axis. In the given figure, the straight line graph from t = 6 s to t = 10 s represents the uniform motion of the car. The part of graph representing uniform motion has been labelled AB.
Q. 9. State which of the following situations are possible and give an example for each of these:
(a) an object with a constant acceleration but with zero velocity
(b) an object moving with an acceleration but with uniform speed.
(c) an object moving in a certain direction with an acceleration in the perpendicular direction.
Answer (a) :-
Yes, it is possible for an object to have constant (non-zero) acceleration while its instantaneous velocity is zero — but only for a brief moment.
Here’s how:
Think of an object thrown straight up into the air. As it rises, gravity acts on it with a constant downward acceleration (approximately (9.8 , \text{m/s}^2)). The object slows down as it climbs, because velocity and acceleration are in opposite directions.
At the very top of its path, the object’s velocity becomes zero — just for an instant — before it starts falling back down. During that entire motion, however, the acceleration due to gravity remains constant and non-zero.
So the example is:
An object thrown vertically upward.
- Velocity at the highest point: 0 m/s
- Acceleration at the highest point: ( -9.8 ms-2downward)
Answer (b):-
Yes, it’s possible for an object to accelerate while maintaining uniform speed, as long as the direction of motion is changing. That’s the key.
🌍 Example: Uniform Circular Motion
Imagine a car moving at a constant speed around a circular track.
- The speed (magnitude of velocity) stays the same.
- But the direction of velocity keeps changing as the car goes around the curve.
- Since velocity is a vector (it has both magnitude and direction), any change in direction is still a change in velocity, which means there’s acceleration.
This acceleration is called centripetal acceleration, and it always points toward the center of the circle.
Summary:
✅ Possible: Yes
🔁 Speed: Constant
🌀 Acceleration: Present (due to changing direction)
📌 Example: Car moving in a circle, or a stone tied to a string being whirled around.
Answer (c):-
Yes, it is absolutely possible! And this concept sits right at the intersection of motion and vector understanding.
💡 Think of it this way:
If an object is moving in one direction (say, forward), and it experiences an acceleration at right angles (perpendicular) to that direction, the result is a curved path.
🎯 Classic Example: Projectile Motion
Imagine a ball being thrown horizontally from the edge of a cliff.
- It moves horizontally with constant speed.
- But the only force acting on it is gravity, which pulls it downward — perpendicular to its initial motion.
So, while the horizontal velocity stays constant, gravity causes the vertical velocity to increase, bending the ball’s path into a curved trajectory — a parabola.
Summary:
✅ Possible? Yes
📌 Direction of motion: Horizontal
📌 Acceleration: Vertical (due to gravity)
🌀 Result: A curved (parabolic) path — classic projectile motion
Q. 10. An artificial satellite is moving in a circular orbit of radius 42250 km. Calculate its speed if it takes 24 hours to revolve around the earth.
Answer:-
